: 그래프의 한 종류로, Root 노드를 기준으로 노드간 Edge로 연결된 트리모양의 자료구조
트리 조건
- 하나의 루트노드를 갖는다.
- 0개 이상의 자식 node를 갖는다.
- 자식 node는 또 재귀적으로 0개 이상의 자식 node를 갖는다.
- cycle이 존재하지 않는다.
- 서로 다른 두 node간 경로는 오직 한 가지 존재한다.
- 그래프의 한 종류이다. 트리는 사이클이 없는 하나의 연결 그래프이다.
- 특정 노드에서 다른 모든 노드로 접근 가능
면접에서의 트리
: 일반적으로 세부사항이 모호하거나 가정 자체가 틀린 경우가 많다. 필요에 따라 요구사항을 명확하게 물어보기
- 트리 vs 이진 트리: 이진, 삼진, … 을 명확하게 구분
- 이진 트리 vs 이진 탐색 트리: 이진트리를 제시 받았을 때 정렬되어있는가 아닌가의 차이를 명확하게 구분
- 균형 vs 비균형: 비균형의 경우 일반적으로 알려진 복잡도의 효율을 기대하기 어렵다.
- 탐색 - log N과 선형(N)의 차이
- 균형을 맞추기 위한 레드-블랙 트리와 AVL 트리가 있다.
이진 힙
: 최소 힙과 최대 힙
핵심 연산
- 삽입
- 언제나 밑바닥에 삽입
- 최소(최대) 힙을 만족하는지 확인 후 Root노드와 새 노드 위치 변경하는 방식
- 제거 - 최소 원소 뽑아내기(최소 힙의 경우)
- Root를 제거한 후 가장 leaf의 노드를 Root에 채워넣기
- 최소(최대) 힙을 만족하는지 확인 후 Root 노드를 자식 노드 중 하나와 교환(더 조건에 부합하는 노드)
트라이
: 접두사 트리.(prefix tree)
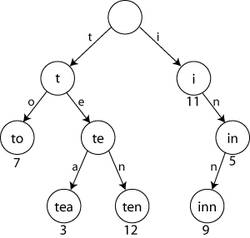
- 각 노드에 문자를 저장한다.
- 아래쪽부터 순회하면 단어 하나가 나오게 된다.
- null node(
* node)를 만나면 단어의 끝이라고 판단.- 위의 그림에서 각 단어(to, tea, ten 등)의 자식 노드에는 * 노드가 존재할 것
- 접두사를 빠르게 찾아보기 위한 흔한 방식
- e.g) “github”이라는 단어를 찾으려고 하는데 “gi”까지 검색했을 때 “gi” 라는 접두사를 갖는 단어가 무엇이 있는지를 찾으려고 할 때
그래프
: 단순히 Node와, 그 Node를 edge로 모아놓은 것
- 방향성이 있을 수도, 없을 수도 있다.
- 순환 그래프, 비순환 그래프 존재
인접 리스트
: 그래프를 표현하는 일반적인 방법
- 모든 정점을 리스트에 저장한다.
- 무방향 그래프라면 간선은 두번 저장된다.(a->b, b->a)
- 트리에선 한 트리 내의 특정 노드에서 다른 모든 노드로 접근이 가능했지만, (방향이 있는)그래프에선 불가능한 경우가 있다.
- 배열이나 연결리스트를 이용해 인접 리스트 표현 가능
인접 행렬
- NxN 불리언 행렬로,
matrix[i][j]가 true이면 i에서 j로 간선이 있다는 뜻 - 무방향이라면 대칭 행렬일 것이고, 방향이라면 대칭이지 않을 수 있다.
탐색 방법 - BFS, DFS
- 사용되는 자료구조가 다를 수 있음(큐, 스택)
- 이전에 방문했는지를 반드시 체크해야한다.(무한루프방지)
- 전위, 후위, 중위 순회의 경우 DFS에 속한다고 보면 된다.
예상 문제
트리에서 각 레벨에 존재하는 노드를 연결리스트로 연결해주는 알고리즘 설계
- 레벨 갯수가 D라면 D개의 연결 리스트가 존재해야한다.
- 현재 순회중인 노드의 깊이만 알 수 있으면 그 깊이인 n번째의 연결리스트에 추가하면 된다.
균형 확인 - 이진트리가 균형이 잡혀있는지를 확인하자
- Root부터 시작해 왼쪽, 오른쪽 노드의 길이 차가 1 이하인지 재귀적으로 확인한다.
Reference)
코딩 인터뷰 완전분석
